Recommender Systems through Collaborative Filtering
Manojit Nandi2017-07-14 | 15 min read

This is a technical deep dive into the collaborative filtering algorithm and how to use it in practice.
From Amazon recommending products you may be interested in based on your recent purchases to Netflix recommending shows and movies you may want to watch, recommender systems have become popular across many applications of data science. Like many other problems in data science, there are several ways to approach recommendations. Two of the most popular are collaborative filtering and content-based recommendations.
- Collaborative Filtering: For each user, recommender systems recommend items based on how similar users liked the item. Let's say Alice and Bob have similar interests in video games. Alice recently played and enjoyed the game Legend of Zelda: Breath of the Wild. Bob has not played this game, but because the system has learned that Alice and Bob have similar tastes, it recommends this game to Bob. In addition to user similarity, recommender systems can also perform collaborative filtering using item similarity ("Users who liked this item also liked X").
- Content-based Recommendations: If companies have detailed metadata about each of your items, they can recommend items with similar metadata tags. For example, let's say I watch the show Bojack Horseman on Netflix. This show may have metadata tags of "Animated", "Comedy", and "Adult", so Netflix recommends other shows with these metadata tags, such as Family Guy.
In this blog post, I will focus on the first approach of collaborative filtering, but also briefly discuss the second approach of content-based recommendations. This is the first post in a series of blog posts on recommender systems for data scientists, engineers, and product managers looking to implement a recommendation system.
Collaborative Filtering-Based Recommendations
The idea behind collaborative filtering is to recommend new items based on the similarity of users. In this section, I will discuss
- How to measure the similarity between users or objects.
- Using the cosine similarity to measure the similarity between a pair of vectors
- How to use model-based collaborative filtering to identify similar users or items.
- Using Surprise, a Python library for simple recommendation systems, to perform item-item collaborative filtering.
Measuring Similarity
If I gave you the points (5, 2) and (8, 6) and ask you to tell me how far apart are these two points, there are multiple answers you could give me. The most common approach would be to calculate the Euclidean distance (corresponding to the length of the straight-line path connecting these two points) and say they are 5 units apart. An alternative approach would be to calculate the Manhattan distance and say they are 7 units apart.
When we compute similarity, we are going to calculate it as a measure of "anti-distance". The higher the distance between two objects, the more "farther apart" they are. On the other hand, the higher the similarity between two objects, the more "closer together" they are. Usually, similarity metrics return a value between 0 and 1, where 0 signifies no similarity (entirely dissimilar) and 1 signifies total similarity (they are exactly the same).
Cosine Similarity
Now, let's discuss one of the most commonly used measures of similarity, the cosine similarity. If I gave you the vectors U = (3,4) and V = (1,1), you could easily tell me how far apart these two vectors are (once again, by using Euclidean distance or some other metric). Now, here's the important question: How similar are these two vectors?
Once again, with similarity, we want a metric of "anti-distance" that falls between 0 and 1. If you recall from trigonometry, the range of the cosine function goes from -1 to 1. Some important properties of cosine to recall:
- Cosine(0°) = 1
- Cosine(90°) = 0
- Cosine(180°) = -1
With the cosine similarity, we are going to evaluate the similarity between two vectors based on the angle between them. The smaller the angle, the more similar the two vectors are.
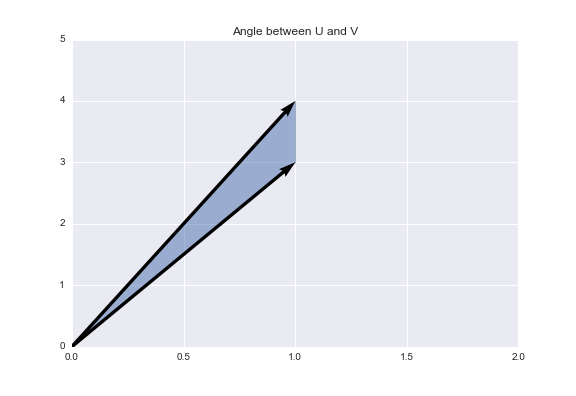
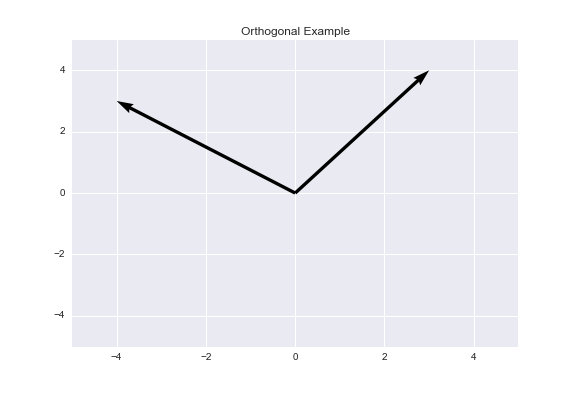
Using cosine similarity, we get that two vectors achieve maximum similarity when the angle between them is 0° (they are oriented in the same direction), they have 0 similarity when the angle between them is 90° (they are orthogonal to one another), and they have -1 similarity when the angle between them is 180° (they are oriented in diametrically opposing directions). Below is an example of orthogonal vectors. The angle between them is 90°, so the cosine similarity is 0.
If we restrict our vectors to non-negative values (as in the case of movie ratings, usually going from a 1-5 scale), then the angle of separation between the two vectors is bound between 0° and 90°, corresponding to cosine similarities between 1 and 0, respectively. Therefore, for positive-valued vectors, the cosine similarity returns a value between 0 and 1, one of the 'ideal' criteria for a similarity metric. One important thing to note is the cosine similarity is a measure of orientation, not magnitude. Two vectors can be oriented in the exact same direction (and thus have cosine similarity of 1) but have different magnitudes.
For example, the vectors (3,4) and (30,40) are oriented in the same direction, but they have different magnitudes (the latter vector is a multiple of the former). It's important when working with cosine similarity to remember that just because two vectors have a similarity score of 1 does not mean they are the same!
Model-Based Collaborative Filtering
Now that we have a concrete method for defining the similarity between vectors, we can now discuss how to use this method to identify similar users. The problem set-up is as follows:
1.) We have an n X m matrix consisting of the ratings of n users and m items. Each element of the matrix (i, j) represents how user i rated item j. Since we are working with movie ratings, each rating can be expected to be an integer from 1-5 (reflecting one-star ratings to five-star ratings) if user i has rated movie j, and 0 if the user has not rated that particular movie.
2.) For each user, we want to recommend a set of movies that they have not seen yet (the movie rating is 0). To do this, we will effectively use an approach that is similar to weighted K-Nearest Neighbors.
3.) For each movie j user i has not seen yet, we find the set of users U who are similar to user i and have seen movie j.
For each similar user u, we take u's rating of movie j and multiply it by the cosine similarity of user i and user u. Sum up these weighted ratings, divide by the number of users in U, and we get a weighted average rating for the movie j.
4.) Finally, we sort the movies by their weighted average rankings. These average rankings serve as an estimate for what the user will rate each movie. Movies with higher average rankings are more likely to be favored by the user, so we will recommend the movies with the highest average rankings to the user.
I said earlier that this procedure is similar to a weighted K-Nearest Neighbors algorithm. We take the set of users who have seen movie j as the training set for K-NN and each user who has not seen the movie as a test point. For each user who has not seen the movie (test point), we compute the similarity to users who have seen the movie, and assign an estimated rating based on the known ratings of the neighbors.
For a concrete example, let's say I have not seen the movie Hidden Figures. I have seen and rated (on a 5-star scale) a ton of other movies though. With this information, you want to predict what I will rate Hidden Figures. Based on my rating history, you can find a group of users who rate movies similarly to me and have also seen Hidden Figures. To keep this example simple, let's say we look at the two users who are most similar to me and have seen the movie. Let's say User 1 has 95% similarity to me and gave the movie a four-star rating, and User 2 has 80% similarity to me and gave the movie a five-star rating. Now my predicted rating is the average of 0.954 = 3.8 (Similarity X Rating of User 1) and 0.805 = 4 (Similarity X Rating of User 2), so I am predicted to give the movie a rating of 3.9.
Surprise
Rather than implementing this procedure by hand ourselves, we are going to use the Surprise library, a Python library for simple recommendation systems.
We'll be working with the MovieLens dataset, a common benchmark dataset for recommendation system algorithms. With the Surprise library, we can load the MoviesLens 100k dataset, which consists of 100,000 movie ratings from about 1,000 users and 1,700 movies.
from surprise import Dataset, evaluate
from surprise import KNNBasicThe Dataset method allows us to easily download and store the MovieLens 100k data in a user-movie interaction matrix. The rows of this matrix represent users, and the columns represent movies. Using this load_builtin method, we get a sparse matrix with 943 rows and 1682 columns.
data = Dataset.load_builtin("ml-100k")
trainingSet = data.build_full_trainset()For our task, we want to use the cosine similarity between movies to make new recommendations. Although I explained collaborative filtering based on user similarity, we can just as easily use item-item similarity to make recommendations. With item-item collaborative filtering, each movie has a vector of all its ratings, and we compute the cosine similarity between two movies' rating vectors.
sim_options = {
'name': 'cosine',
'user_based': False
}
knn = KNNBasic(sim_options=sim_options)Now, we can train our model on our training data set.
knn.train(trainingSet)Now that we have trained our model, we want to make movie recommendations for users. Using the build_anti_testset method, we can find all user-movie pairs in the training set where the user has not viewed the movie and create a "testset" out of these entries.
testSet = trainingSet.build_anti_testset()
predictions = knn.test(testSet)Since our model will make dozens of movie recommendations for each user, we are going to use a helper method to get only the top three movie recommendations for each user.
from collections import defaultdict
def get_top3_recommendations(predictions, topN = 3):
top_recs = defaultdict(list)
for uid, iid, true_r, est, _ in predictions:
top_recs[uid].append((iid, est))
for uid, user_ratings in top_recs.items():
user_ratings.sort(key = lambda x: x[1], reverse = True)
top_recs[uid] = user_ratings[:topN]
return top_recsIn our dataset, each user and movie is represented with an ID number. If we were to view the output of our model now, we would receive a list of movie IDs for each user; not a result we can easily interpret. Therefore, we will use a second helper method read_item_names to create a dictionary that maps each movie's ID to its name. This method is based on one of the examples in the Surprise library's Github repo.
import os, io
def read_item_names():
"""Read the u.item file from MovieLens 100-k dataset and returns amapping to convert raw ids into movie names."""
file_name = (os.path.expanduser('~') +'/.surprise_data/ml-100k/ml-100k/u.item')rid_to_name = {}
with io.open(file_name, 'r', encoding='ISO-8859-1') as f:
for line in f:
line = line.split('|')
rid_to_name[line[0]] = line[1]
return rid_to_nameNow, we can call our get_top3_recommendations method to get the top movie recommendations for each user and output the result.
top3_recommendations = get_top3_recommendations(predictions)
rid_to_name = read_item_names()
for uid, user_ratings in top3_recommendations.items():
print(uid, [rid_to_name[iid] for (iid, _) in user_ratings])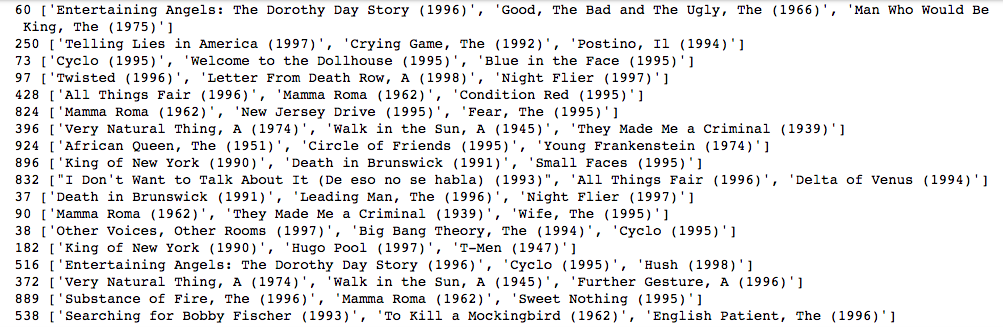
As you can see, each user receives personalized movie recommendations based on how they rated the movies they have seen.
One of the major weaknesses of collaborative filtering is known as the cold-start problem: How do we make recommendations to new users whom we have little to no data about their preferences? Since we have no information about the user's preferences, we cannot accurately compute the similarity between the new user and more established users.
Content-Based Recommendation
In this section, I will briefly discuss how content-based recommendations work. In the previous section, we discussed using the cosine similarity to measure how similar two users are based on their vectors. Let's say we want to determine how similar a pair of items are based on their metadata tags. For example, with movies, metadata tags could be information about actors or actresses in the movie (Dwayne Johnson), genre (Action), and director (J.J Abrams).
The Jaccard similarity gives us a measure of similarity between two sets by counting the number of items they have in common and dividing by the total number of unique items between them. Essentially, it's the ratio of the number of items they both share compared to the number of items they could potentially share. In formal mathematical terms, the Jaccard similarity between two sets A and B is the cardinality, or the number of elements, in the intersect of A and B divided by the cardinality of the union of A and B.
Now that we have a measure of similarity based on each item's meta-data tags, we can easily recommend new items to the user. Let's say I watch the movie Zootopia on Netflix. Because Netflix has extensive meta-data tags for the shows and movies on its platform, Netflix can compute the Jaccard similarity between Zootopia and shows and movies I have not seen yet. After computing the similarities, it can then recommend new movies to me that are similar to Zootopia, such as Finding Dory.
Of course, this is not the only way to perform content-based filtering. There are plenty of other methods we can use to analyze each item's meta-data. With Natural Language Processing techniques such as TF-IDF or topic modeling, we can analyze the descriptions of movies and define a measure of similarity between movies based on similar TF-IDF vectors or topic models.
Like collaborative filtering, content-based recommendations suffer if we do not have data on our user's preferences. If we don't have any information about what a new user is interested in, then we can't make any recommendations, regardless of how detailed our metadata is.
Conclusion
With enough data, collaborative filtering provides a powerful way for data scientists to recommend new products or items to users. If you have well-detailed metadata about your products, you could also use a content-based approach to recommendations.
For those of you who are interested in learning more about recommender systems, I highly encourage you to check out the chapter on Recommender Systems in the Mining Massive Dataset book.
In an upcoming blog post, I will demonstrate how we can use matrix factorization to produce recommendations for users, and then I will showcase a hybrid approach to recommend using a combination of the aspects of collaborative filtering and content-based recommendations. This hybrid method resolves the weaknesses of both collaborative filtering and content-based recommendation.
Manojit is a Senior Data Scientist at Microsoft Research where he developed the FairLearn and work to understand data scientist face when applying fairness techniques to their day-to-day work. Previously, Manojit was at JPMorgan Chase on the Global Technology Infrastructure Applied AI team where he worked on explainability for anomaly detection models. Manojit is interested in using my data science skills to solve problems with high societal impact.



