Domino recently added support for GPU instances. To celebrate this release, I will show you how to:
- Configure the Python library Theano to use the GPU for computation.
- Build and train neural networks in Python.
Using the GPU, I'll show that we can train deep belief networks up to 15x faster than using just the CPU, cutting training time down from hours to minutes.
Why are GPUs useful?
When you think of high-performance graphics cards, data science may not be the first thing that comes to mind. However, computer graphics and data science have one important thing in common: matrices!
Images, videos, and other graphics are represented as matrices, and when you perform a certain operation, such as a camera rotation or a zoom in effect, all you are doing is applying some mathematical transformation to a matrix.
What this means is that GPUs, compared to CPUs (Central Processing Unit), are more specialized at performing matrix operations and other advanced mathematical transformations. In some cases, we see a 10x speedup in an algorithm when it runs on the GPU.
GPU-based computation have been employed in a wide variety of scientific applications, from genomic to [epidemiology].
Recently, there has been a rise in GPU-accelerated algorithms in machine learning thanks to the rising popularity of deep learning algorithms. Deep Learning is a collection of algorithms for training neural network-based models for various problems in machine learning. Deep Learning algorithms involve computationally intensive methods, such as convolutions, Fourier Transforms, and other matrix-based operations which GPUs are well-suited for computing. The computationally intensive functions, which make up about 5% of the code, are run on the GPU, and the remaining code is run on the CPU.
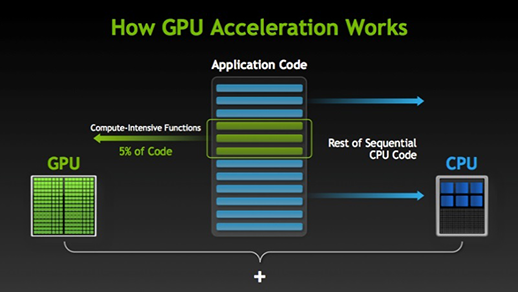
Source: Nvidia
With the recent advances in GPU performance and support for GPUs in common libraries, I recommend anyone interested in deep learning get ahold of a GPU.
Now that I have thoroughly motivated the use of GPUs, let's see how they can be used to train neural networks in Python.
Deep Learning in Python
The most popular library in Python to implement neural networks is Theano. However, Theano is not strictly a neural network library, but rather a Python library that makes it possible to implement a wide variety of mathematical abstractions. Because of this, Theano has a high learning curve, so I will be using two neural network libraries built on top of Theano that have a more gentle learning curve.
The first library is Lasagne. This library provides a nice abstraction that allows you to construct each layer of the neural network, and then stack the layers on top of each other to construct the full model. While this is nicer than Theano, constructing each layer and then appending them on top of one another becomes tedious, so we'll be using the Nolearn library which provides a Scikit-Learn style API over Lasagne to easily construct neural networks with multiple layers.
Because these libraries do not come default with Domino's hardware, you need to create a requirements.txt with the following text:
pip install -r https://raw.githubusercontent.com/dnouri/nolearn/master/requirements.txt git+https://github.com/dnouri/nolearn.git@master#egg=nolearn==0.7.gitSetting up Theano
Now, before we can import Lasagne and Nolearn, we need to [configure Theano, so that it can utilize the GPU hardware. To do this, we create a .theanorc file in our project directory with the following contents:
[global]
device = gpu
floatX = float32
[nvcc]
fastmath = TrueThe .theanorc file must be placed in the home directory. On your local machine, this could be done manually, but we cannot access the home directory of Domino's machine, so we will move the file to the home directory using the following code:
import os
import shutil
destfile = "/home/ubuntu/.theanorc"
open(destfile, 'a').close()
shutil.copyfile(".theanorc", destfile)The above code creates an empty .theanorc file in the home directory and then copy the contents of the .theanorc file in our project directory into the file in the home directory.
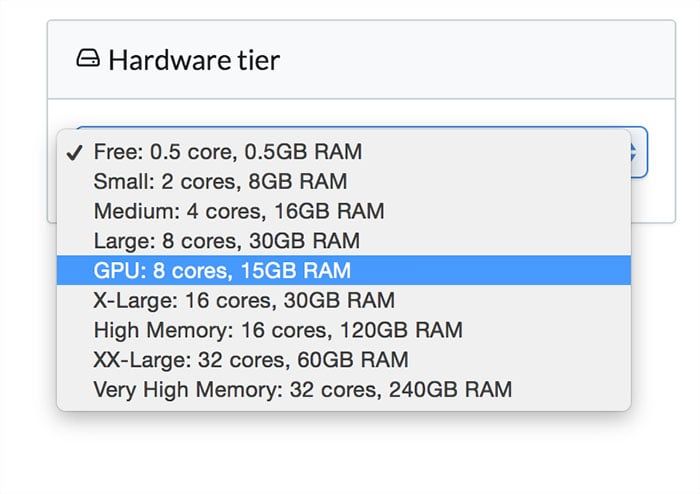
After changing the hardware tier to GPU, we can test to see if Theano detects the GPU using the test code provided in Theano's documentation.
from theano import function, config, shared, sandbox
import theano.tensor as T
import numpy
import time
vlen = 10 * 30 * 768 # 10 x #cores x # threads per core
iters = 1000
rng = numpy.random.RandomState(22)
x = shared(numpy.asarray(rng.rand(vlen), config.floatX))
f = function([], T.exp(x))
print(f.maker.fgraph.toposort())
t0 = time.time()
for i in xrange(iters):
r = f()
t1 = time.time()
print('Looping %d times took' % iters, t1 - t0, 'seconds')
print('Result is', r)
if numpy.any([isinstance(x.op, T.Elemwise) for x in f.maker.fgraph.toposort()]):
print('Used the cpu')
else:
print('Used the gpu')If Theano detects the GPU, the above function should take about 0.7 seconds to run and will print 'Used the gpu'. Otherwise, it will take 2.6 seconds to run and print 'Used the cpu'. If it outputs this, then you forgot to change the hardware tier to GPU.
The Dataset
For this project, we'll be using the CIFAR-10 image dataset containing 60,000 32x32 colored images from 10 different classes.

Fortunately, the data come in a pickled format, so we can load the data using helper functions to load each file into NumPy arrays to produce a training set (Xtr), training labels (Ytr), testing set (Xte), and testing labels (Yte). Credit for the [following code]goes to Stanford's CS231n course staff.
import cPickle as pickle
import numpy as np
import os
def load_CIFAR_file(filename):
'''Load a single file of CIFAR'''
with open(filename, 'rb') as f:
datadict= pickle.load(f)
X = datadict['data']
Y = datadict['labels']
X = X.reshape(10000, 3, 32, 32).transpose(0,2,3,1).astype('float32')
Y = np.array(Y).astype('int32')
return X, Y
def load_CIFAR10(directory):
'''Load all of CIFAR'''
xs = []
ys = []
for k in range(1,6):
f = os.path.join(directory, "data_batch_%d" % k)
X, Y = load_CIFAR_file(f)
xs.append(X)
ys.append(Y)
Xtr = np.concatenate(xs)
Ytr = np.concatenate(ys)
Xte, Yte = load_CIFAR_file(os.path.join(directory, 'test_batch'))
return Xtr, Ytr, Xte, YteMulti-Layered Perceptron
A multi-layered perceptron is one of the most simple neural network models. The model consists of an input layer for the data, a hidden layer to apply some mathematical transformation, and an output layer to produce a label (either categorical for classification or continuous for regression).
Before we can use the training data, we need to grayscale it and flatten it into a two-dimensional matrix. In addition, we will divide each value by 255 and subtract 0.5. When we grayscale the image, we convert each (R,G,B) tuple in a float value between 0 and 255. By dividing by 255, we normalize the grayscale value to the interval [0,1]. Next, we subtract 0.5 to map the values to the interval [-0.5, 0.5]. Now, each image is represented by a 1024-dimensional array where each value is between -0.5 and 0.5. It's common practice to standardize your input features to the interval [-1, 1] when training classification networks.
X_train_flat = np.dot(X_train[...,:3], [0.299, 0.587, 0.114]).reshape(X_train.shape[0],-1).astype(np.float32)
X_train_flat = (X_train_flat/255.0)-0.5
X_test_flat = np.dot(X_test[...,:3], [0.299, 0.587, 0.114]).reshape(X_test.shape[0],-1).astype(np.float32)
X_test_flat = (X_test_flat/255.0)-.5Using Nolearn's API, we can easily create a multi-layered perceptron with an input, hidden, and output layer. The hidden_num_units = 100 means our hidden layer has 100 neurons, and the output_num_units = 10 means our output layer has 10 neurons, one for each of the label. Before outputting, the network applies a softmax function to determine the most probable label. If The network is trained for 50 epochs and with verbose = 1, the model prints out the result of each training epoch and how long the epoch took.
net1 = NeuralNet(
layers = [
('input', layers.InputLayer),
('hidden', layers.DenseLayer),
('output', layers.DenseLayer),
],
#layers parameters:
input_shape = (None, 1024),
hidden_num_units = 100,
output_nonlinearity = softmax,
output_num_units = 10,
#optimization parameters:
update = nesterov_momentum,
update_learning_rate = 0.01,
update_momentum = 0.9,
regression = False,
max_epochs = 50,
verbose = 1,)As a side remark, this API makes it easy to build deep networks. If we wanted to add a second hidden layer, all we would have to do is add it to the layers parameter and specify how many units in the new layer.
net1 = NeuralNet(
layers = [
('input', layers.InputLayer),
('hidden1', layers.DenseLayer),
('hidden2', layers.DenseLayer), #Added Layer Here
('output', layers.DenseLayer),
],
#layers parameters:
input_shape = (None, 1024),
hidden1_num_units = 100,
hidden2_num_units = 100, #Added Layer Params HereNow, as I mentioned earlier about Nolearn's Scikit-Learn style API, we can fit the Neural Network with the fit method.
net1.fit(X_train_flat, y_train)When the network is trained on the GPU hardware, we see each training epoch usually takes 0.5 seconds.
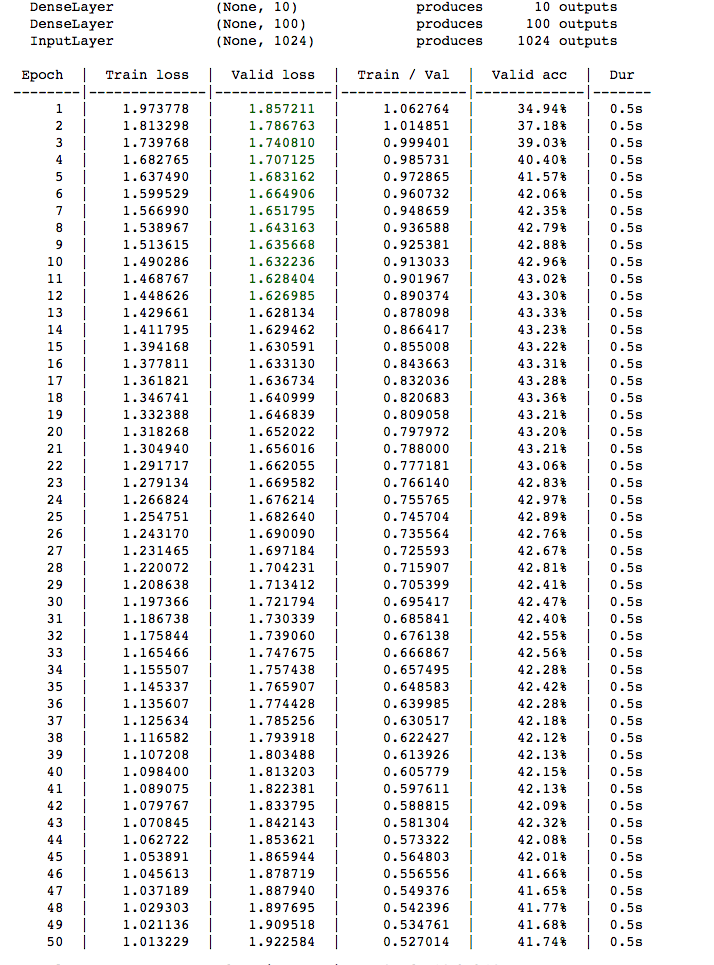
On the other hand, when Domino's hardware is set to XX-Large (32 core, 60 GB RAM), each training epoch takes usually takes 1.3 seconds.
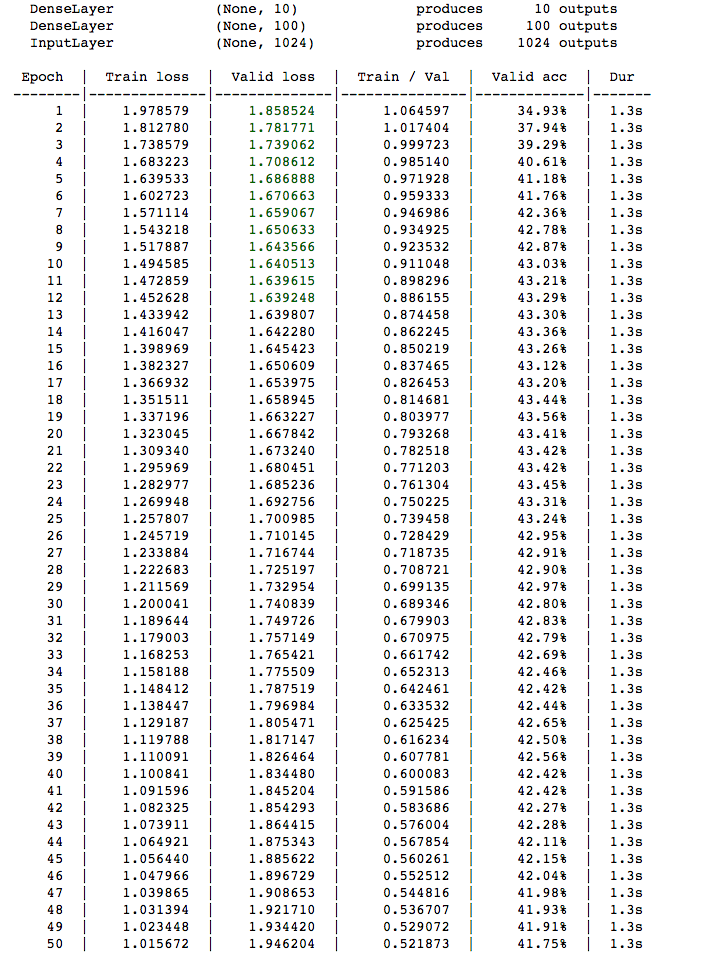
By training this network on the GPU, we see roughly a 3x speedup in training the network. As expected, both the GPU-trained network and the CPU-trained network yield similar results. Both yield about a similar validation accuracy of 41% and similar training loss.
We can test the network on the testing data:
y_pred1 = net1.predict(X_test_flat)
print("The accuracy of this network is: %0.2f" % (y_pred1 == y_test).mean())And we achieve an accuracy of 41% on the testing data.
Convolutional Networks
A convolutional neural network is a more complex neural network architecture in which neurons in a layer are connected to a subset of neurons from the previous layer. As a result, convolutions are used to pool the outputs from each subset.
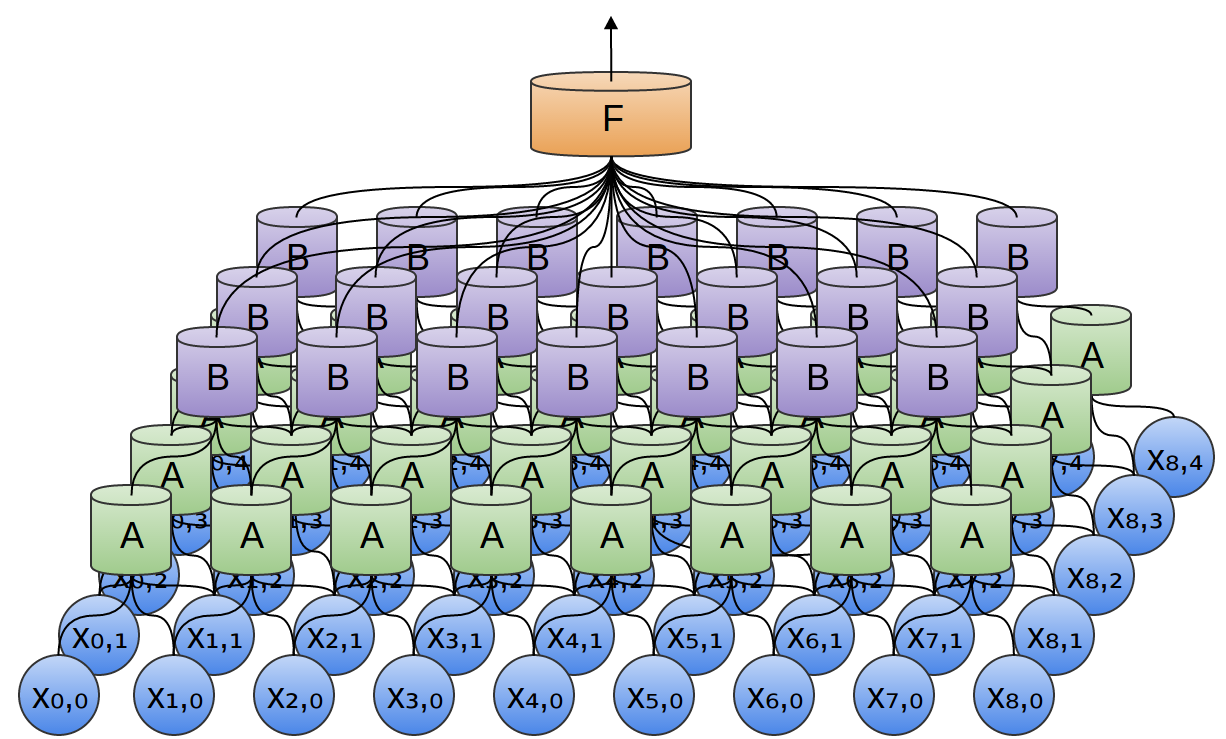
Source: http://colah.github.io/posts/2014-07-Conv-Nets-Modular/
Convolutional Neural Networks are popular in industry and Kaggle Competitions due to their flexibility to learn different problems and scalability.
Once again, before we can build our convolutional neural network, we have to first grayscale and transform the data. This time we will keep the images in their 32x32 shape. I have modified the order of the rows of the matrix, so each image is now represented as (color, x, y). Once again, I divide the features by 255, and subtract by 0.5 to map the features within the interval (-1, 1).
X_train_2d = np.dot(X_train[...,:3], [0.299, 0.587, 0.114]).reshape(-1,1,32,32).astype(np.float32)
X_train_2d = (X_train_2d/255.0)-0.5
X_test_2d = np.dot(X_test[...,:3], [0.299, 0.587, 0.114]).reshape(-1,1,32,32).astype(np.float32)
X_train_2d = (X_train_2d/255.0)-0.5Now we can construct the Convolutional Neural Network. The Network consists of the input layer, 3 convolution layers, 3 2x2 pooling layers, a 200-neuron hidden layer, and finally the output layer.
net2 = NeuralNet(layers = [
('input', layers.InputLayer),
('conv1', layers.Conv2DLayer),
('pool1', layers.MaxPool2DLayer),
('conv2', layers.Conv2DLayer),
('pool2', layers.MaxPool2DLayer),
('conv3', layers.Conv2DLayer),
('pool3', layers.MaxPool2DLayer),
("hidden4", layers.DenseLayer),
("output", layers.DenseLayer),],
#layer parameters:
input_shape = (None, 1, 32, 32),
conv1_num_filters = 16, conv1_filter_size = (3, 3), pool1_pool_size = (2,2),
conv2_num_filters = 32, conv2_filter_size = (2, 2) , pool2_pool_size = (2,2),
conv3_num_filters = 64, conv3_filter_size = (2, 2), pool3_pool_size = (2,2),
hidden4_num_units = 200,
output_nonlinearity = softmax,
output_num_units = 10,
#optimization parameters:
update = nesterov_momentum,
update_learning_rate = 0.015,
update_momentum = 0.9,
regression = False,
max_epochs = 5,
verbose = 1,
)
Once again, we can fit the model using the fit method.
net2.fit(X_train_2d, y_train)Compared to the Multi-Layer Perceptron, the Convolutional Neural Network will take longer to train. With the GPU enabled, most training epochs take 12.8 seconds to complete. However, the Convolutional Neural Network achieves a validation loss of about 63%, beating the Multi-Layered Perceptron's validation loss of 40%. So by incorporating the convolution and pooling layers, we can improve our accuracy by 20%.
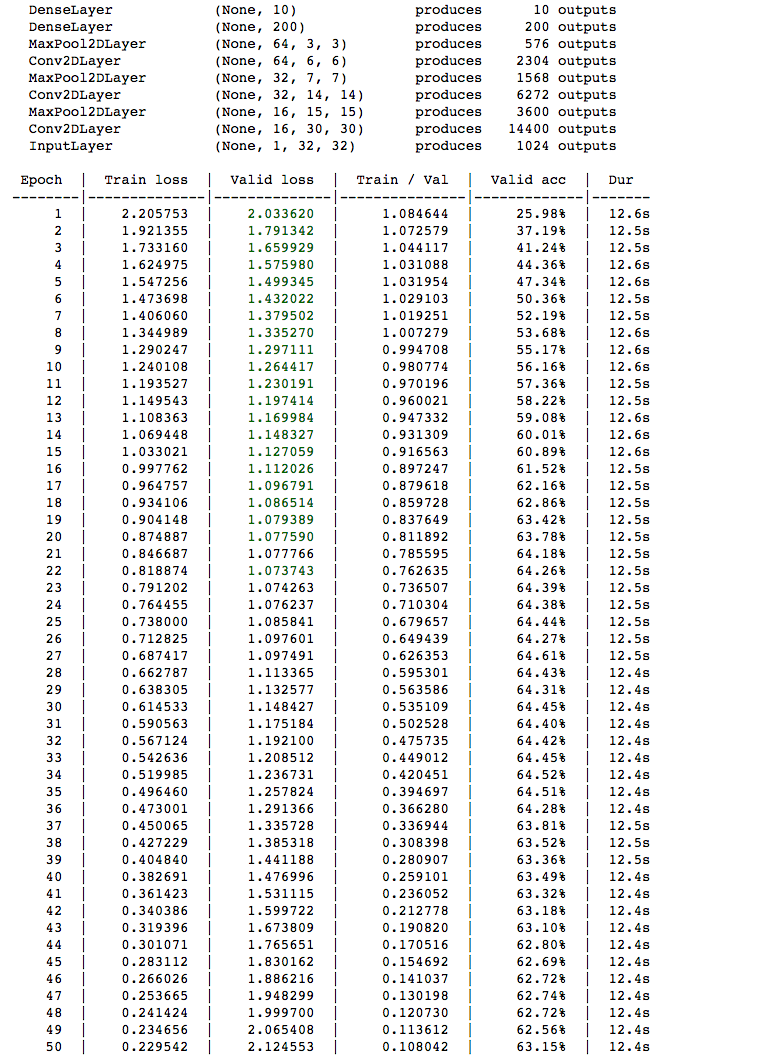
With only the CPU on Domino's XX-Large Hardware tier, each training epoch takes about 177 seconds, or close to 3 minutes, to complete. Thus, by training using the GPU, we see about a 15x speedup in the training time.
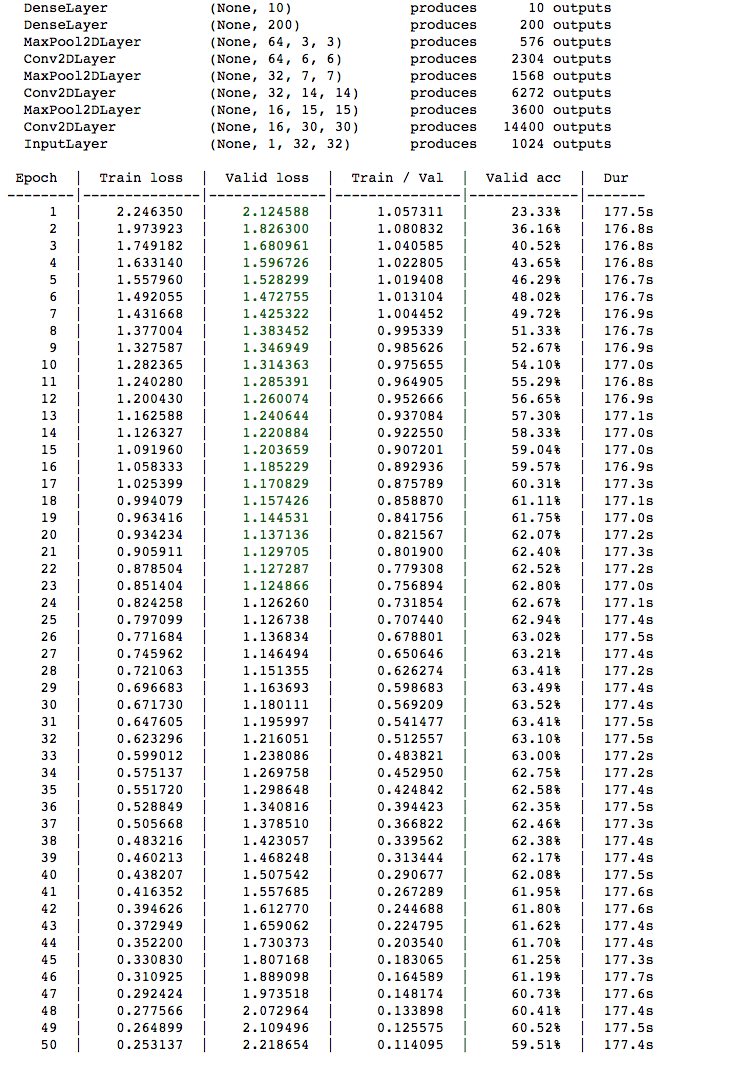
Once again, we see similar results for the Convolutional Neural Network trained on the CPU compared to the Convolutional Neural Network trained on the GPU, with similar validation accuracies and training losses.
When we test the convolutional neural network on the testing data, we achieve an accuracy of 61%.
y_pred2 = net2.predict(X_test_2d)
print("The accuracy of this network is: %0.2f" % (y_pred2 == y_test).mean())Using the GPU to train deep neural networks results in a speedup in runtime, ranging from 3x faster to 15x faster in this project. In industry and academia, we often use multiple GPUs as this cuts the training runtime of deep networks down from weeks to days.
Additional Resources
NVIDIA has launched a free online course on GPUs and deep learning, so those of who are interested in learning more about GPU-accelerated deep learning can check this course out!
Additionally, Udacity has a free online course in CUDA Programming and Parallel Programming for those who are interested in general GPU and CUDA programming.
If you are more interested in convolutional neural networks, the Neural Networks and Deep Learning ebook recently released a chapter on convolutional neural network.
I would like to extend a special acknowledgement to Reddit user sdsfs23fs for their criticism and correcting incorrect statements I had in my original version of this blog post. In addition, this Reddit user provided me with code for the image pre-processing step that greatly improves the accuracy of the neural networks.
Edit: I have updated the requirements.txt file for this project to overcome an error caused by one of the Python libraries. The new requirements.txt is listed above in the Deep Learning in Python section.
Manojit is a Senior Data Scientist at Microsoft Research where he developed the FairLearn and work to understand data scientist face when applying fairness techniques to their day-to-day work. Previously, Manojit was at JPMorgan Chase on the Global Technology Infrastructure Applied AI team where he worked on explainability for anomaly detection models. Manojit is interested in using my data science skills to solve problems with high societal impact.
Subscribe to the Domino Newsletter
Receive data science tips and tutorials from leading Data Science leaders, right to your inbox.
By submitting this form you agree to receive communications from Domino related to products and services in accordance with Domino's privacy policy and may opt-out at anytime.



