
Many types of real-world problems involve dependencies between records in the data. For example, sociologist are eager to understand how people influence the behaviors of their peers; biologists wish to learn how proteins regulate the actions of other proteins. Problems involving dependencies can often be modeled as graphs, and scientists have developed methods for answering these questions called network analysis.
This post describes how to use the Python library NetworkX, to deal with network data and solve interesting problems in network analysis.
Intro to Graphs
Before we dive into a real-world network analysis, let's first review what a graph is. A graph consists of a set of objects V called vertices and a set of edges E connecting pairs of vertices.
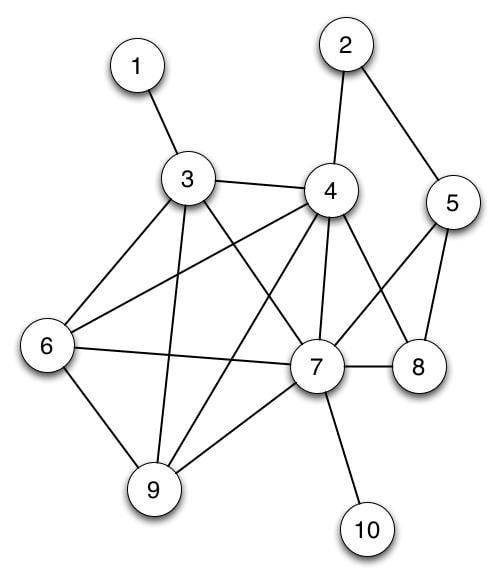
In the above picture, the circles represent the vertices and lines connecting the circles are edges. If this graph represented a social network, the circles would represent people, and an edge between two vertices could signify that those two individuals are friends.
We will look at a special type of network called an ego network. In an ego network, there is a "central" vertex or the ego vertex which the network revolves around.
Ego networks are important in sociology because they allow researchers to study the structure of an individual's relationships with respect to his world.
Getting started with NetworkX
import networkx as nxDomino offers NetworkX as one of its default Python libraries, so all you have to do is import the library with the above statement.
Now, let's consider a real-world dataset: Facebook Ego Networks!
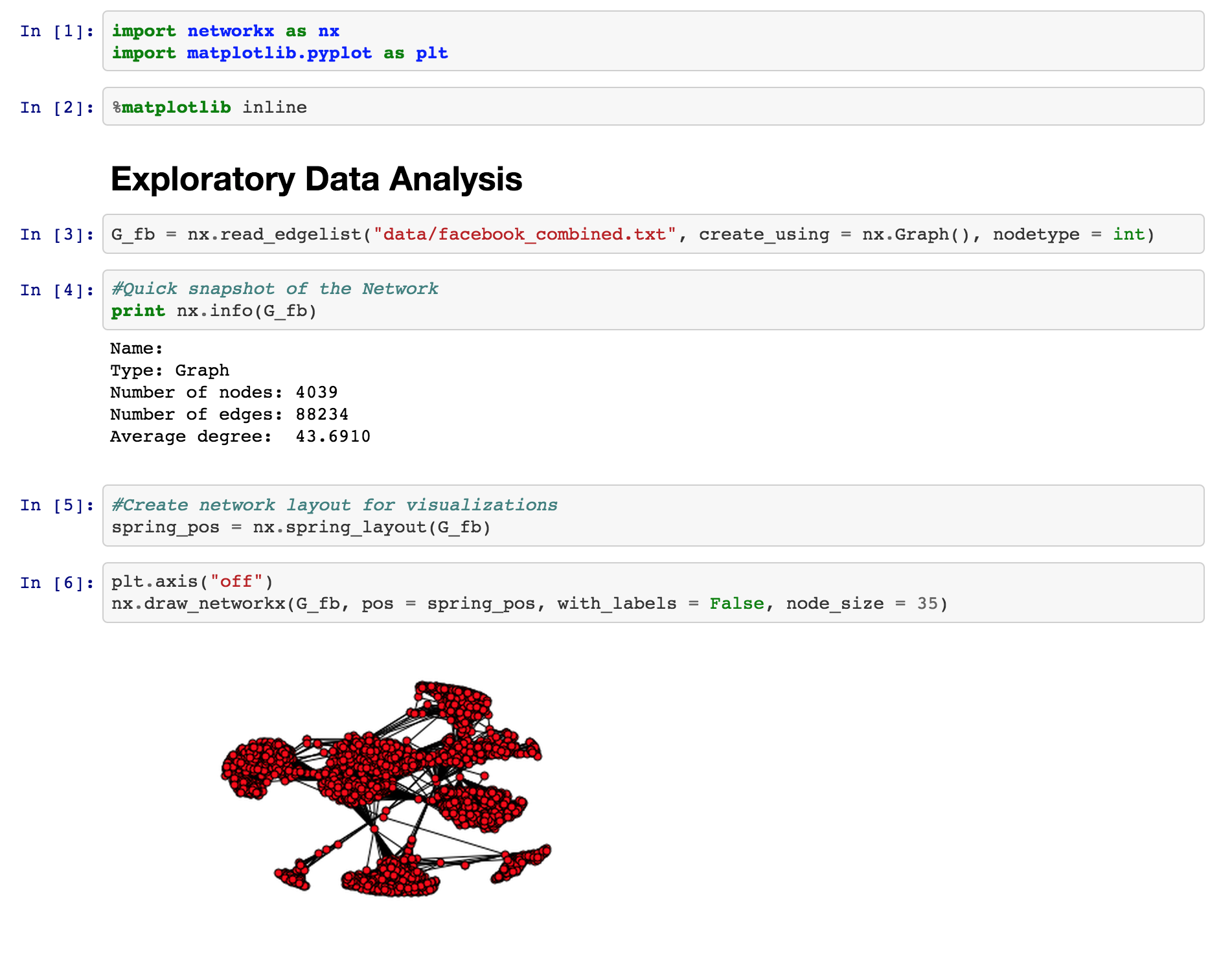
This Facebook combined ego networks datasets contains the aggregated network of ten individuals' Facebook friends list. In this dataset, the vertices represent individuals on Facebook, and an edge between two users means they are Facebook friends. Each ego-network was created by starting with a Facebook user and then mining all of his Facebook friends. The ego-networks are then aggregated by identifying individuals who appear in multiple ego-networks.
Here's some basic information about the network dataset we will be working with:
- Nodes: 4039
- Edges: 88,234
- Average Degree: 43.6910

As you can see this is a fairly connected network, and the number of edges in the network is more than 20x the number of nodes, so the network is densely clustered. If you examine the network, you will notice certain hubs of vertices appear. Hubs like these are an important feature of real-world social networks. Dense hubs represent high clustering and are often the result of underlying social mechanisms that are of interest to scientists.
Parallel Betweenness
How do we determine who is the most "important" individual in the network. Well, that depends on the definition of "important". One way to define "importance" is the individual's betweenness centrality. The betweenness centrality is a measure of how many shortest paths pass through a particular vertex. The more shortest paths that pass through the vertex, the more central the vertex is to the network.
Because the shortest path between any pair of vertices can be determined independently of any other pair of vertices, we can take advantage of Domino's multi-core hardware to compute the betweenness centrality of each vertex in the network using a parallelized algorithm.
To do this, we will use the Pool object from the multiprocessing library and the itertools library. A nice introduction to the multiprocessing library and parallel programming in Python can be found here.
from multiprocessing import Pool
import itertoolsFirst thing we need to do is partition the vertices of the network into n subsets where n is dependent on the number of processors we have access to. For example, if we use a machine with 32 cores, we partition the Facebook network in 32 chunks with each chunk containing 128 vertices.
Now instead of one processor computing the betweenness for all 4,039 vertices, we can have 32 processors computing the betweenness for each of their 128 vertices in parallel. This drastically reduces the run-time of the algorithm and allows it to scale to larger networks.
def partitions(nodes, n):
"Partitions the nodes into n subsets"
nodes_iter = iter(nodes)
while True:
partition = tuple(itertools.islice(nodes_iter,n))
if not partition:
return
yield partition
# To begin the parallel computation, we initialize a Pool object with the
# number of available processors on our hardware. We then partition the
# network based on the size of the Pool object (the size is equal to the
# number of available processors).
def between_parallel(G, processes = None):
p = Pool(processes=processes)
part_generator = 4*len(p._pool)
node_partitions = list(partitions(G.nodes(), int(len(G)/part_generator)))
num_partitions = len(node_partitions)
#Next, we pass each processor a copy of the entire network and
#compute #the betweenness centrality for each vertex assigned to the
#processor.
bet_map = p.map(btwn_pool,
zip([G]*num_partitions,
[True]*num_partitions,
[None]*num_partitions,
node_partitions))
#Finally, we collect the betweenness centrality calculations from each
#pool and aggregate them together to compute the overall betweenness
#centrality score for each vertex in the network.
bt_c = bet_map[0]
for bt in bet_map[1:]:
for n in bt:
bt_c[n] += bt[n]
return bt_cNow, let's look at the vertices with the top 10 highest betweenness centrality measures in the network.

As you can see, vertices that primarily either sit at the center of a hub or acts a bridge between two hubs have higher betweenness centrality. The bridge vertices have high betweenness because all paths connecting the hubs pass through them, and the hub center vertices have high betweenness because all intra-hub paths pass through them.
Community Detection
For those of you who use Facebook, your Facebook friends probably come from different aspects of your life: Some are your friends from college, others are your co-workers, and maybe some old friends from your hometown.
Because your friends can be broken down into different groups like this, you may wonder if we could identify these different communities in your social network. The answer is yes! Using community detection algorithms, we can break down a social network into different potentially overlapping communities.
The criteria for finding good communities is similar to that for finding good clusters. We want to maximize intra-community edges while minimizing inter-community edges. Formally, the algorithm tries to maximize the modularity of network, or the fraction of edges that fall within the community minus the expected fraction of edges if the edges were distributed by random. Good communities should have a high number of intra-community edges, so by maximizing the modularity, we detect dense communities that have a high fraction of intra-community edges.
While there is no community detection method in NetworkX, a good samaritan has written a community detection library built on top of NetworkX.
import communityThis library is easy to use and allows to perform community detection on an undirected graph in less than 3 lines of code!
parts = community.best_partition(G_fb)
values = [parts.get(node) for node in G_fb.nodes()]That's all there is to it!
Now let's look at the different communities.

As you can see, the communities closely align with the vertex hubs. Because this dataset was compiled by aggregating the ego network of ten individuals, the different communities most likely reflect the different ego networks.
Conclusion
Graphs and networks are becoming more popular in data science everyday. Neo4j is a database that represents data as a graph, and topological data analysis algorithms and spectral clustering algorithms build upon graphs to identify flexible patterns and sub-structures in data.
You can use Domino to run network algorithms on large hardware to speed up your calculations.
Manojit is a Senior Data Scientist at Microsoft Research where he developed the FairLearn and work to understand data scientist face when applying fairness techniques to their day-to-day work. Previously, Manojit was at JPMorgan Chase on the Global Technology Infrastructure Applied AI team where he worked on explainability for anomaly detection models. Manojit is interested in using my data science skills to solve problems with high societal impact.
RELATED TAGS
Subscribe to the Domino Newsletter
Receive data science tips and tutorials from leading Data Science leaders, right to your inbox.
By submitting this form you agree to receive communications from Domino related to products and services in accordance with Domino's privacy policy and may opt-out at anytime.



